Derivations used in rivr

Michael Koohafkan

Introduction

This vignette documents the mathematical derivations for gradually-varied and unsteady flow analysis with rivr. All derivations are based on Chaudry (2007). In Section 1, important definitions related to channel geometry are discussed. In Section 2, basic concepts of open-channel flow are discussed and one-dimensional shallow-water equations are derived. In Section 3, gradually-varied flow is derived and the standard-step method is discussed. In Section 4, the kinematic and dynamic wave models for simulating unsteady flow are derived along with the three discretization methods available in rivr. Finally, Section 5 discusses the Method of Characteristics and its application to boundary conditions of unsteady flow simulations.

Section 1: Channel geometry relations

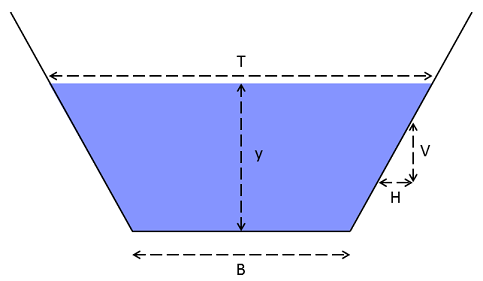
A channel is prismatic if it has the same slope and cross-section throughout its entire length. The rivr package currently supports prismatic trapezoidal channels of arbitrary bottom width $B$ and side slope $SS = H:V$. Given a flow depth $y$, the flow area is then $$A = By + SSy^2$$ Another important definition is the wetted perimeter $P$, which for a trapezoidal cross-section is $$P = B + 2y\sqrt{1 + SS^2}$$ The hydraulic radius is the ratio of the cross-sectional flow area to the wetted perimeter, i.e. $$R = \frac{A}{P}$$ The hydraulic depth $D$ is defined as the ratio of the cross-sectional flow area to the top width $T$, where $$T = \frac{dA}{dy}$$ which for a trapezoidal cross-section yields $$T = B + 2ySS$$ and $$D = \frac{A}{T} = \frac{By + SSy^2}{B + 2ySS}$$ Finally, the term $\bar{y}$ is related to hydrostatic pressure and is defined as the distance from the water surface to the centroid of the cross-sectional flow area, i.e. $$\bar{y} = \frac{2B + T}{3(B + T)} y$$

The definitions described above are fundamental properties related to one-dimensional open-channel flow. These relations (and their derivatives) are used extensively in the following sections to derive important flow relations and appear repeatedly in numerical solution schemes.

Section 2: Basic concepts of one-dimensional open-channel flow

The flow depth of a channel in an equilibrium state is called the normal depth, i.e. the flow depth at which gravitational forces (bed slope) are balanced by friction forces (bed roughness). The rivr package expresses the normal depth via the semi-empirical Manning’s equation $$Q = \frac{C_m}{n} AR^{2/3}S_0^{1 / 2}$$ where $Q$ is the channel flow, $S_0$ is the channel slope, $A$ is the cross-sectional flow area, $R$ is the hydraulic depth and $C_m$ is a conversion factor based on the unit system used (1.49 in US customary units and 1.0 in SI units). The expression is often rewritten as $$Q = KS_0^{1 / 2}$$ Where $K$ is the channel conveyance. The normal depth $y_n$ factors into the expressions of both $A$ and $R$ (i.e. $K$) and the above equation cannot be rearranged to solved explicitly for the normal depth; an implicit (iterative) solution is needed. The univariate Netwon-Raphson method is often used to provide efficient and precise solutions for $y_n$. Generally, the Newton-Raphson method is defined as $$x = x^* - \frac{f(x^*)}{\frac{df}{dx}\bigg|_{x^*}}$$ where $x$ is the updated guess for the parameter for which a solution is sought, $x^*$ is the prior guess for the parameter value, $f(x)$ is a zero-valued function of the parameter and $\frac{df}{dx}$ is the derivative of said function. To apply the Newton-Raphson method here, Manning’s equation is rewritten as $$f(y_n) = AR^{2/3} - \frac{nQ}{C_m S_0^{1 / 2}} = 0$$ and its derivative is $$\frac{df}{dy_n} = \frac{5}{3}T R^{2/3} - \frac{2}{3}R^{5/3}\frac{dP}{dy_n}$$ where $\frac{dP}{dy_n} = 2\sqrt{1 + SS^2}$. A related concept is the critical depth, the flow depth which minimizes the specific energy of the flow. The specific energy is the sum of flow depth and velocity head, i.e. $$E = y + \frac{u^2}{2g} = \frac{1}{2g}\left(\frac{Q}{A}\right)^2$$ where $u$ is the uniform flow velocity. The critical depth is then the flow depth that satisfies $$\frac{dE}{dy} = 0 = 1 - \frac{Q^2}{gA^3}\frac{dA}{dy} = 1 - \frac{Q^2 T}{gA^3}$$ For a trapezoidal channel it can be mathematically proved that only one critical depth exists for a given flow rate. The critical depth can be solved using the Newton-Raphson method with $f(y_c) = \frac{dE}{dy} = 0$ and $$\frac{df}{dy_c} = \frac{3}{2}\left(AT\right)^{1 / 2} - \frac{1}{2}\left(\frac{A}{T}\right)^{3/2}\frac{dT}{dy_c}$$ where $\frac{dT}{dy_c} = 2SS$ for a trapezoidal channel. The critical depth is also the depth at which the Froude number of the flow is unity; the Froude number is a dimensionless measure of bulk flow characteristics that represents the relative importance of inertial forces and gravitational forces and is defined as $$Fr = \frac{Q}{A\sqrt{gD}}$$

Flows are referred to as subcritical if the flow depth is greater than the critical depth ($Fr < 1$) and supercritical if the flow depth is less than the critical depth ($Fr > 1$). Flows can transition gradually from subcritical to supercritical conditions; when the rate of variation of flow depth is small with respect to the longitudinal distance over which the change occurs, the river state is referred to as gradually-varied flow. In contrast, the transition from supercritical to subcritical conditions occur abruptly in the form of a hydraulic jump and is an example of rapidly-varied flow. Both gradually-varied and rapidly-varied flows can be either steady (flow is constant through time) or unsteady (flow rate varies with respect to time). The rivr package provides solutions for steady gradually-varied and unsteady flow problems.

Section 3: Solutions to steady gradually-varied flow problems

The standard-step method can be used to solve the steady gradually-varied flow profile when the channel flow and geometry are known. Additionally, the flow depth $y$ must be known at a specified channel cross-section; this cross-section is referred to as the control section and the flow depth associated with the channel flow rate $Q$ at the control section is $y_1$. The total head $H_1$ at the control section is the sum of the elevation head, flow depth head, and velocity head, i.e. $$H_1 = y_1 + z_1 + \frac{1}{2g}\left(\frac{Q}{A_1}\right)^2 = z_1 + E_1$$ where $z_1$ is the elevation of the control section bottom relative to some datum and $A_1$ is the cross-sectional flow area at the control section. From conservation of energy, it follows that the total head $H_2$ at some downstream cross-section, referred to as the target section, is $$H_2 = H_1 - h_f$$ where $h_f$ is the head loss. While the head loss term generally combines both friction loss and form drag, the latter component is neglected by rivr. The friction component is expressed as the average friction slope between the control and target sections: $$h_f = \frac{{S_f}_1 + {S_f}_2}{2} \left(x_2 - x_1\right)$$ where $x_2 - x_1$ is the longitudinal distance between the control and target section. Note that the sign of $h_f$ therefore depends on whether the control section is upstream ($x_1 < x_2$) or downstream ($x_1 > x_2$) of the target section. Substituting these terms into the governing equation and rearranging yields $$y_2 + z_2 + \frac{1}{2g}\left(\frac{Q}{A_2}\right)^2 + \frac{{S_f}_1 + {S_f}_2}{2} \left(x_2 - x_1\right) = y_1 + z_1 + \frac{1}{2g}\left(\frac{Q}{A_1}\right)^2$$ Note that all terms on the right-hand side of the equation are known, while $A_2$ and ${S_f}_2$ on the left-hand side of the equation are functions of $y_2$. Transposing all terms to the left-hand side yields a zero-value function of $y_2$: $$f(y_2) = 0 = y_2 + z_2 + \frac{1}{2g}\left(\frac{Q}{A_2}\right)^2 + \frac{{S_f}_1 + {S_f}_2}{2} \left(x_2 - x_1\right) - y_1 - z_1 - \frac{1}{2g}\left(\frac{Q}{A_1}\right)^2$$ This function is suitable for solving using the Newton-Raphson method discussed previously, i.e. $$y_2 = y_2^* - \frac{f(y_2^*)}{\frac{df}{dy}\bigg|_{y_2^*}}$$ where $$\frac{df}{dy_2} = 1 - \frac{Q^2}{gA_2^3}\frac{dA_2}{dy_2} + \frac{1}{2}\left(x_2 - x_1\right) \frac{d{S_f}_2}{dy_2}$$ and $$\frac{d{S_f}_2}{dy} = -2\left(\frac{{S_f}_2}{A} \frac{dA}{dy} + \frac{2}{3} \frac{{S_f}_2}{R} \frac{dR}{dy} \right)$$ Once the flow depth at the target section is found, the target section becomes the new control section and the flow depth at the next target section is computed, with the algorithm “stepping” up or down the channel to a specified distance from the initial control section. The standard-step method is accessed via the function compute_profile.

Section 4: Solutions to unsteady-flow problems

Unsteady flow problems are generally characterized using the Shallow Water Equations, with the one-dimensional form expressed as $$\frac{\partial A}{\partial t} + \frac{\partial Q}{\partial x} = 0$$$$\frac{\partial Q}{\partial t} + \frac{\partial}{\partial x} \left(Qu + g\bar{y}A\right) - gA\left(S_0 - S_f\right) = 0$$ where the first equation expresses mass conservation and the second expresses momentum conservation. Without further simplification, these equations are often referred to as the Dynamic Wave Model (DWM). The Kinematic Wave Model (KWM) refers to a simplification of the momentum equation by assuming $S_0 = S_f$, i.e. the momentum equation is instead expressed through the relation $$A = \left( \frac{nQP^{2/3}}{C_m S_0^{1 / 2}} \right)^{3/5}$$ Both the KWM and DWM can be solved using numerical discretization methods such as finite-difference schemes. Finite-difference schemes discretize a continuous model domain into a series of nodes separated by an incremental distance $\Delta x$. The model time domain is similarly discretized into a series of time steps separated by an incremental time $\Delta t$. A finite-difference scheme is called explicit if the value of the variable being solved for on time step $k + 1$ depends explicitly on the value of the variable at the previous time step $k$. Explicit methods are advantageous because they are easier to program and implement, but are disadvantageous because they are subject to stability constraints. The stability constraint is defined by the Courant number $$C = \frac{\Delta t}{\Delta x} u$$ which represents the ratio of the flow velocity to the rate of propagation of information through the model domain. The numerical solution is unstable if $C > 1$.

The rivr package provides an interface to one finite-difference numerical scheme for the KWM and two finite-difference schemes for the DWM. In addition, the DWM interface supports boundary condition solutions using the Method of Characteristics (MOC). These schemes are accessed via the function route_wave and their derivations are discussed below.

Solution to the Kinematic Wave Model

The KWM finite-difference scheme implemented in rivr requires a constant time step and spatial resolution, a known upstream boundary condition (flow) for the full simulation time, and an initial condition (flow) at every node. The initial water depth, flow area, and flow velocity are calculated from the channel geometry relations, with the initial water depth assumed to be the normal depth. At the initiation of a new time step $k + 1$, the flow at the upstream boundary node $i = 1$ is assigned from the user-supplied boundary condition. The flow depth at the upstream boundary is calculated as the normal depth for that flow, i.e. $$y_1^{k+1} = y_n\left(Q_1^{k+1}\right)$$ where the superscripts denote the timestep. The flow at a downstream node $i$ is computed as $$Q_i^{k+1} = Q^{k+1}_{i - 1} - \frac{\Delta x}{\Delta t}\left( A_{i-1}^{k+1} - A_{i-1}^{k}\right)$$ where the subscripts denote the node. The flow depth at node $i$ is calculated using a Newton-Raphson formulation where $$f(y_i^{k+1}) = 0 = A_i^{k+1} - \left(\frac{nQ_i^{k+1}}{C_m S_0^{1 / 2}}\right)^{3/5} \left(P_i^{k+1}\right)^{2/5}$$
and $$\frac{df}{dy_i^{k+1}} = \frac{dA}{dy}\bigg|_{y_i^{k+1}} - \frac{2}{5}\frac{dP}{dy}\bigg|_{y_i^{k+1}} \left( \frac{nQ_i^{k+1}}{C_m S_0^{1 / 2} P_i^{k+1}} \right)^{3/5}$$ Once the flow depth is known, the remaining geometry relations can be computed and the algorithm moves to the next downstream node. The algorithm advances to the next time step once all nodes are computed.

Solution to the Dynamic Wave Model: the Lax diffusive scheme

The set of equations describing the DWM are more complex than the KWM, and therefore requires more sophisticated numerical solution methods. The Lax diffusive scheme is similar to the scheme used for the KWM in terms of the model domain discretization and initialization, but requires additional computations at each node to obtain the solution.

For an internal (non-boundary) node $i$ on time step $k + 1$, flow values are computed through a two step process. First, averages of $A$, $Q$, and the inertial term $S = gA\left(S_f - S_0\right)$ are computed for the node, i.e. $$A_i^* = \frac{1}{2}\left(A^k_{i+1} + A^k_{i - 1} \right)$$$$Q^*_i = \frac{1}{2}\left(Q^k_{i+1} + Q^k_{i - 1} \right)$$$$S_i^* = \frac{1}{2}\left(S^k_{i+1} + S^k_{i - 1}\right) = \frac{gA}{2}\left({S_f}^k_{i + 1} + {S_f}^k_{i - 1} - 2S_0\right)$$ The values for node $i$ on time step $k + 1$ are then calculated as $$A_i^{k + 1} = A_i^* - \frac{\Delta t}{2\Delta x}\left(Q^k_{i+1} - Q^k_{i-1}\right)$$$$Q_i^{k + 1} = Q_i^* - \frac{\Delta t}{2\Delta x}\left(F^k_{i+1} - F^k_{i-1}\right) - S_i^*\Delta t$$ where $F = Qu + g\bar{y}A$. To compute the flow depth $y_i^{k+1}$ from the new area $A_i^{k+1}$, the Newton-Raphson method is again applied where $$f(y_i^{k+1}) = 0 = A\left(y_i^{k+1}\right) - A_i^{k+1}$$ and $$\frac{df}{dy_i^{k+1}} = \frac{dA}{dy} \bigg|_{y_i^{k+1}}$$ It is clear from the derivation that unlike the KWM solution, both the upstream and the downstream boundary conditions must be known at each time step. The MOC described later provides a method for predicting, rather than imposing, the downstream boundary condition.

Solution to the Dynamic Wave Model: the MacCormack scheme

The MacCormack scheme is an advanced finite-differencing scheme that provides high accuracy for considerably coarser spatial and temporal resolutions compared to the Lax diffusive scheme. The scheme consists of a backwards-looking predictor step followed by a forward-looking corrector step. The intermediate values calculated in the predictor step are used to develop new intermediate values in the corrector step, and these calculations are averaged to obtain the final value. The predictor step computes the intermediate values at an internal node $i$ as $$Q_i^* = Q_i^k - \frac{\Delta t}{\Delta x}\left( F_i - F_{i - 1}\right) - S_i^k \Delta t$$$$A^*_i = A_i^k - \frac{\Delta t}{\Delta x}\left( Q_i^k - Q_{i-1}^k \right)$$ with intermediate values of $F$ and $S$ ($F^*$ and $S^*$) computed from these results. On the corrector step, new values for $Q$ and $A$ are computed as $$Q_i^{**} = Q_i^{k} - \frac{\Delta t}{\Delta x}\left( F^*_{i + 1} - F^*_{i} \right) - S_i^* \Delta t$$$$A_i^{**} = A_i^k - \frac{\Delta t}{\Delta x}\left( Q_{i+1}^* - Q_i^* \right)$$ The new values for time step $k + 1$ are the arithmetic averages of the predictor and corrector step results, i.e. $Q_i^{k+1} = \frac{1}{2}\left( Q_i^* + Q_i^{**} \right)$ and $A_i^{k+1} = \frac{1}{2}\left( A_i^* + A_i^{**} \right)$. The remaining terms are then computed from these new values.

Solutions to boundary conditions: the Method of Characteristics

The DWM solution schemes provided by rivr require that both the upstream and downstream boundary be known. Because the downstream boundary is not known a priori under many circumstances, the requirement would limit the utility of the numerical schemes. The Method of Characteristics (MOC) provides a method for predicting the downstream boundary condition at the beginning of each time step, allowing users to route waves trhough the downstream boundary with minimal loss of information. In addition, the method also allows the user to specify both the upstream and downstream boundary conditions in terms of either flow or depth, and allows specification of sudden cessation of flow, i.e. closure of a sluice gate at the upstream or downstream boundary.

MOC is a well-known concept with application to a wide variety of numerical problems; the general theory is not presented here. It can be shown that the upstream boundary condition (node $i = 1$) on time step $k$ can be defined as $$u_1^k = \phi_1^0 + \psi_2^0 y_1^k$$ where $$\psi_2^0 = \sqrt{\frac{g}{y_2^0}}$$ and $$\phi_1^0 = u_2^0 - \psi_2^0 + g\left( S_0 - {S_f}_2^0 \right)\Delta t$$ As seen from these relations, the flow velocity and depth at the upstream boundary on any time step $k$ are related to the initial conditions (i.e.  $k = 0$). The downstream boundary condition (node $i = N$) is similarly expressed as $$u^k_N = \phi_N^0 - \psi_{N-1}^0 y_N^k$$ where $$\psi^0_{N-1} = \sqrt{\frac{g}{y^0_{N-1}}}$$ and $$\phi^0_{N} = u^0_{N-1} + \psi^0_{N-1} y^0_{N-1} + g\left( S_0 - {S_f}^0_{N-1} \right) \Delta t$$ Therefore given either a flow or depth on timestep $k$, the upstream boundary condition can be computed as long as the initial conditions are known. This is a notable improvement over the normal-depth assumption of the upstream boundary condition employed in the KWM. Flow can be routed through the downstream boundary by assuming the gradient in flow or water level between the downstream boundary and the nearest internal node is zero (i.e. $Q^k_N = Q^k_{N-1}$ or $y^k_N = y^k_{N-1}$). This results in “smearing” the solution across the downstream boundary but is often still preferable to direct specification of flow. Specifying the downstream boundary as a constant water depth representing i.e. a lake or reservoir water level may also be appropriate under many circumstances. When flow is specified at e.g. the upstream boundary, flow depth and area are solved simultaneously using a Newton-Raphson scheme where $$f(y_1^k) = Q_1^k - A_1^k \left(\phi_1^0 + \psi_2^0 y_1^k\right) = 0$$ and $$\frac{df}{dy_1^k} = -\frac{dA}{dy}\bigg|_{y_1^k} \left( \phi_1^0 + \psi_2^0 A_1^k + y_1^k \right)$$ Note that if $Q_1^k = 0$ the flow depth $y_1^k$ can be solved for directly, and if depth is supplied then the flow can be solved for directly. The solution method for the downstream boundary is analogous, noting that the sign of the second term in $f(y^k_{N})$ and the corresponding term in its derivative are reversed.